Start of topic | Skip to actions
Berger-Oliger AMR-algorithm
Instead of replacing single cells by finer ones the AMR-method follows a patch-wise refinement strategy (see fig. 1). Cells being flagged by various error estimators are clustered into rectangular boxes of appropriate size. They describe refinement regions geometrically and subgrids with refined mesh spacing in space and time are generated according to them. Refined grids are derived recursively from coarser ones and an entire hierarchy of successively embedded grid patches is therefore constructed. All grid patches are logically rectangular and only a specific integration method for single rectangular grids is required. The adaptive algorithm calls this application dependent routine automatically. Further on it uses conservative interpolation functions to transfer cell values between refined subgrids and their coarser parents appropriately.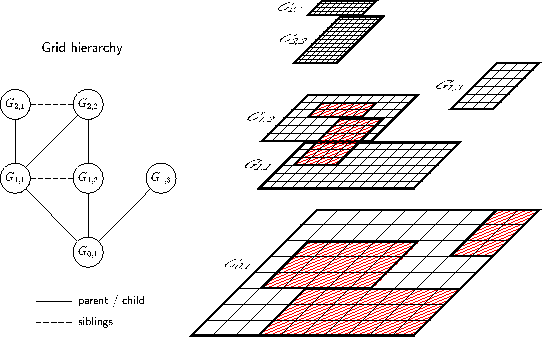 Figure 1: The blockstructured refinement strategy creates a hierarchy of properly nested subgrids.
Figure 1: The blockstructured refinement strategy creates a hierarchy of properly nested subgrids.
It is important to note, that refined grids overlay the coarser subgrids from which they have been created. The numerical solution on a particular level is first of all advanced independently. Values of cells covered by refined subgrids are overwritten by averaged fine grid values subsequently. The resulting extra work is usually negligible compared to the computational costs for integrating the superimposed refinement grids. Replacing coarse cell values by averaged fine grid values modifies the numerical stencil on the coarse grid. In general the import property of conservation is lost. A flux correction replacing the coarse grid flux at the affected side of a neighboring cell by accumulated fine grid fluxes is necessary to ensure conservation. This so called conservative fixup is usually implemented as a correction pass. In two and three space dimensions hanging nodes additionally have to be considered (see fig. 2).
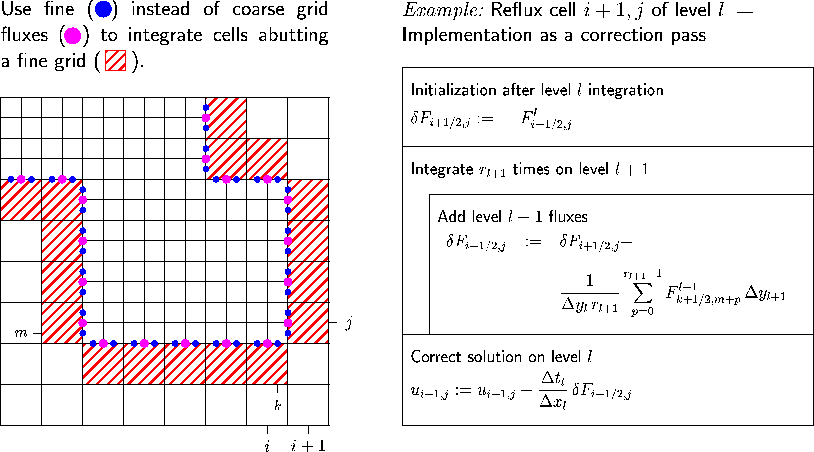 Figure 2: Conservative fixup at fine-to-coarse interfaces.
Figure 2: Conservative fixup at fine-to-coarse interfaces.
An important difference of the AMR approach in comparison to usual unstructured adaptive strategies is the application of refined time-steps on finer subgrids. The algorithm follows a recursive integration procedure that allows the construction of internal boundary conditions for refined subgrids by time-space interpolation (see 3). By applying the same refinement factor in time as in space the CFL number in principle remains unchanged on refined subgrids.
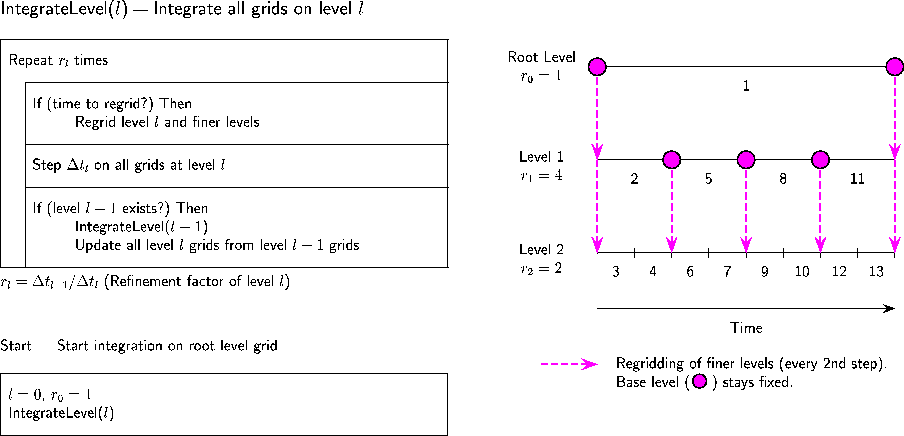 Figure 3: Recursive integration order of the AMR-algorithm.
Figure 3: Recursive integration order of the AMR-algorithm.
-- RalfDeiterding - 11 Dec 2004